Election Blog
Week 9: Final Election Prediction
Part 1: National Two-Party Popular Vote Share
Model formula: $$pv2p_t = \beta_0 + \beta_1\cdot{Economy_t} + \beta_2\cdot{Polling_t} + \beta_3\cdot{Demographics_t} + \beta_4\cdot{Incumbency_t}$$
\(Economy_t\): As Sides & Vavreck (2013) emphasized, fundamentals, such as the state of the economy, play a stronger role than campaign dynamics in determining election outcomes. This is supported by Achen & Bartels (2017), who argued that voters often vote retrospectively based on the economy.
I ran a random forest model to identify the most important economic indicators influencing vote share. To account for historical trends effectively, I incorporated data from 1980 onward, the beginning of the Reagan era, when election factors in significant realignments in American politics, so my model can reflect current ideological divides.
For my super learning model, I selected the five most predictive economic indicators: unemployment rate, GDP growth rate, S&P 500 volume, consumer sentiment index, and RDP growth in the second quarter of the election year.
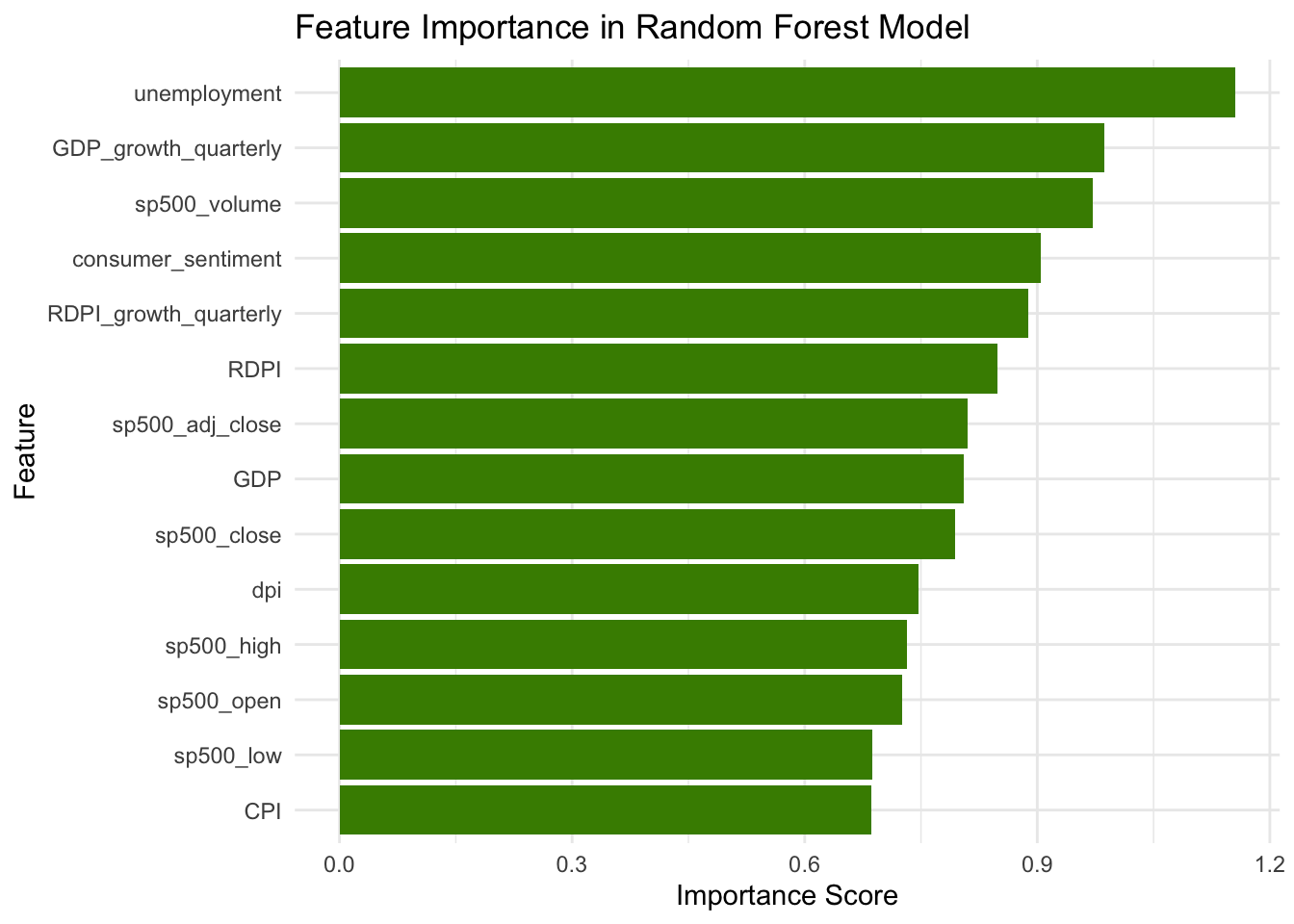
\(Polling_t\): Gelman & King (1993) highlighted that polling closer to the election tends to be more accurate, as it reflects voters’ settled and informed preferences. Tien & Lewis-Beck (2017) also similarly argued that long-view (historical and theoretical) models align closer with the actual popular vote result.
In my model, I used the mean FiveThirtyEight poll averages from three months before the election day and the final poll average immediately before the election. I also obtained Gallup presidential job approval ratings to calculate mean net approval since June and latest net approval ratings in the same manner, informed by Abramowitz’s Time-for-Change Model.
\(Demographics_t\): According to Kim & Zilinsky (2024)’s partisan identification is the strongest and most stable predictor of vote choice. Consistent with this finding, my random forest model reveals that party identification outperform other demographic variables in predictive power.
Therefore, I include partisan affiliation among registered voters as a demographic predictor in my model.
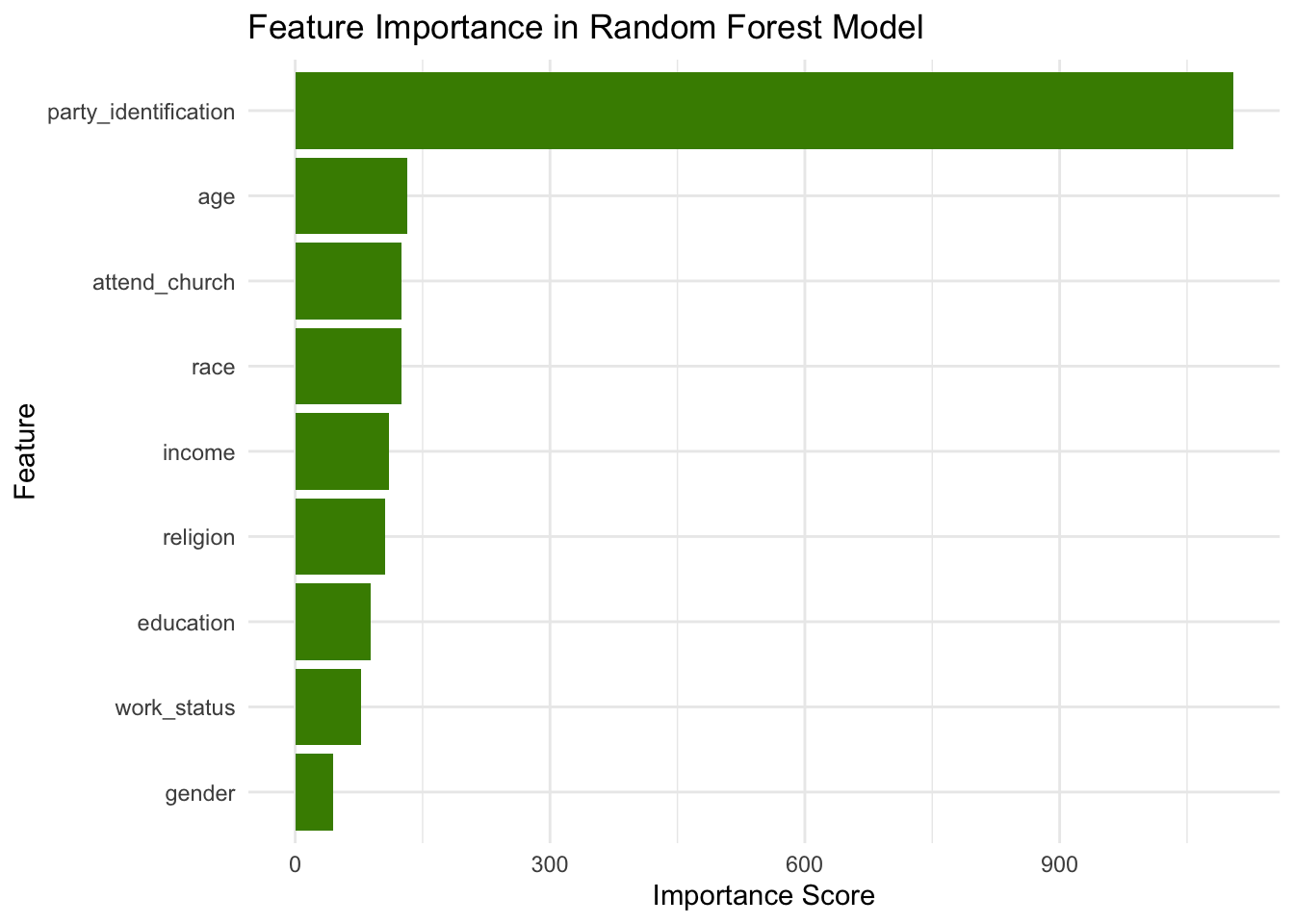
\(Incumbency_t\): Incumbent presidents are typically at an advantage, be it through name recognition, public attention through media coverage, headstart in campaigning without the concern of primary elections, and power for pork-barrel spending. In my model, I do not consider Kamala Harris as an incumbent president (even though she is the current vice president), but I take into account that she is from the incumbent party.
\(AirWar_t\), \(GroundGame_t\), and \(Shocks_t\): After analyzing these variables in my previous blog posts, I found no significant interactions between these dynamic, volatile campaign elements and the actual election outcome. Therefore, I exclude them from my final prediction model.
I use super learning to develop a weighted ensemble where weights are determined by out-of-sample performance of each OLS models with different combination of variables. The tables below show the in-sample and out-of-sample MSEs. The large out-of-sample MSE for the economy model in 2020 is likely due to the outliers in economic indicators as a result of COVID-19, whereas that in 2008 can be attributed to the global financial crisis.
The variation in weights demonstrates the model’s adaptability based on each election’s specific economic and political context. For example, in 2020, the economic data was weighted less heavily, as COVID-19 impacted economic indicators without drastically affecting vote share. In 1992, Clinton’s campaign famously emphasized, “It’s the economy, stupid,” and economic models might have underemphasized public sentiment about Bush’s perceived lack of connection to economic hardship, something that polling picked up through indicators like approval ratings and direct questions about voter preferences.
| Year | In-Sample Economy MSE | In-Sample Polling MSE | In-Sample Demographics MSE | In-Sample Combined MSE | In-Sample Ensemble MSE | Out-of-Sample Economy MSE | Out-of-Sample Polling MSE | Out-of-Sample Demographics MSE | Out-of-Sample Combined MSE | Out-of-Sample Ensemble MSE | Economy Weight | Polling Weight | Demographics Weight | Combined Weight |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020 | 4.837 | 2.8758 | 21.28 | 0 | 5.0185 | 23175.4122 | 0.7734 | 4.2110 | 65497.975 | 0.0000 | 0.0617 | 0.4349 | 0.4644 | 0.0390 |
| 2016 | 12.297 | 2.8880 | 21.53 | 0 | 12.2968 | 0.0083 | 0.4688 | 0.6188 | 378.679 | 0.0083 | 1.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2012 | 12.148 | 1.8683 | 20.99 | 0 | 2.5631 | 4.8623 | 19.6347 | 8.1441 | 23.688 | 0.0000 | 0.2347 | 0.1656 | 0.2160 | 0.3837 |
| 2008 | 3.710 | 1.7232 | 19.31 | 0 | 1.7556 | 2049.0252 | 33.5689 | 31.8964 | 393.809 | 0.0000 | 0.1841 | 0.2782 | 0.2780 | 0.2596 |
| 2004 | 12.268 | 2.7405 | 21.20 | 0 | 4.6760 | 0.3389 | 2.5818 | 5.6484 | 9.561 | 0.0000 | 0.2792 | 0.2241 | 0.3169 | 0.1798 |
| 2000 | 12.189 | 2.9138 | 21.57 | 0 | 5.7391 | 1.9799 | 0.3773 | 0.0064 | 378.679 | 0.0000 | 0.3395 | 0.3189 | 0.3057 | 0.0359 |
| 1996 | 8.265 | 2.7477 | 19.92 | 0 | 2.0482 | 49.3868 | 4.6406 | 24.4830 | 27.598 | 0.0000 | 0.1520 | 0.7434 | 0.0531 | 0.0515 |
| 1992 | 7.884 | 2.9239 | 20.56 | 0 | 2.9239 | 66.0277 | 0.0235 | 14.7096 | 511.620 | 0.0235 | 0.0000 | 1.0000 | 0.0000 | 0.0000 |
| 1988 | 11.576 | 2.5760 | 20.11 | 0 | 0.0000 | 9.1768 | 4.8048 | 21.2632 | 2.737 | 2.7368 | 0.0000 | 0.0000 | 0.0000 | 1.0000 |
| 1984 | 4.109 | 2.8966 | 15.94 | 0 | 0.7683 | 140.7379 | 0.8586 | 78.8061 | 27.595 | 0.0000 | 0.1113 | 0.3089 | 0.1424 | 0.4374 |
| 1980 | 8.975 | 0.9999 | 21.36 | 0 | 4.1401 | 515.1202 | 26.4980 | 3.9181 | 4381.167 | 0.0000 | 0.2166 | 0.3219 | 0.3518 | 0.1098 |
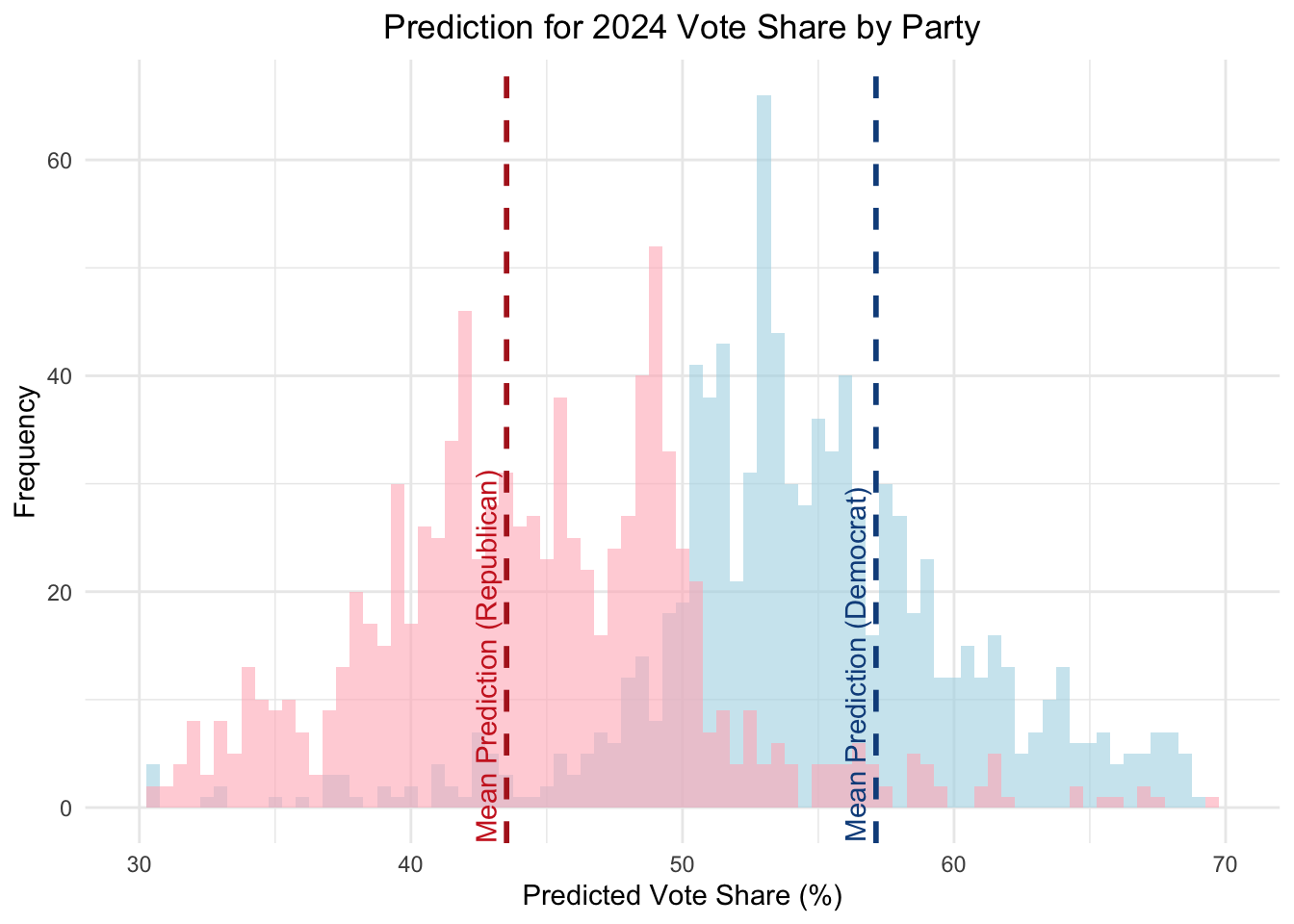
Because the current vote shares do not add up to 100%, I rescaled them to 100%. Overall, I predict that the Democratic Party will receive 56.76% of the national two-party popular vote share, with a 90% prediction interval between 56.5% and 54.55%.
| Year | Party | Predicted Vote Share (%) | Winner |
|---|---|---|---|
| 2024 | Democrat | 56.76 | TRUE |
| 2024 | Republican | 43.24 | FALSE |
Part 2: Electoral College Vote Share
Model formula: $$pv2p_t = \beta_0 + \beta_1\cdot{pv2p_{t-1}} + \beta_2\cdot{pv2p_{t-2}} + \beta_3\cdot{Economy_t} + \beta_4\cdot{Polling_t} + \beta_5\cdot{Incumbency_t}$$
In my state-level model predicting the Democratic Party’s popular vote share, I use a similar set of variables as in my national-level model. This includes economic indicators, polling data, demographics, and incumbency status.
\(pv2p_{t-1} + {pv2p_{t-2}}\): I incorporate the Democratic Party’s vote share from the previous two elections in each state to account for the specific political climate and voter sentiment at the state level.
\(Economy_t\): Including the \(Economy_t\) variable at the state level is tricky as it’s unclear whether voters prioritize sociotropic concerns (national economic indicators) or individual concerns (state economic indicators). To explore this, I compared the significance of these two types of indicators in predicting vote share using a mixed-effects model. Accounting for each state’s baseline political preference, higher state unemployment rates are associated with a significant decrease in the incumbent party’s vote share. This supports the theory that voters are responsive to local economic conditions. Therefore, I included state unemployment as an economic indicator in my model.
| Variable | Estimate | Std. Error | DF | t-value | p-value |
|---|---|---|---|---|---|
| (Intercept) | 49.5386 | 5.1652 | 452 | 9.5909 | 0.0000 |
| state_gdp | 0.0336 | 0.2343 | 452 | 0.1432 | 0.8862 |
| state_unemployment | -1.6802 | 0.5862 | 452 | -2.8661 | 0.0043 |
| natl_gdp | -0.2394 | 0.3273 | 452 | -0.7313 | 0.4650 |
| natl_unemployment | 0.2547 | 0.4671 | 452 | 0.5452 | 0.5859 |
| natl_consumer_sentiment | -0.0357 | 0.0465 | 452 | -0.7692 | 0.4422 |
\(Demographics_t\): Due to lack of a time series data of voter’s party registration and identification at the state-level, I omit this variable from my state-level analysis.
I use super learning to develop a weighted ensemble where weights are determined by out-of-sample performance of each OLS models with different combination of variables.
| Year | In-Sample Lagged Vote MSE | In-Sample Economy MSE | In-Sample Polling MSE | In-Sample Combined MSE | In-Sample Ensemble MSE | In-Sample Lagged Vote MSE | Out-of-Sample Economy MSE | Out-of-Sample Polling MSE | Out-of-Sample Combined MSE | Out-of-Sample Ensemble MSE | Lagged Vote Weight | Economy Weight | Polling Weight | Combined Weight |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2020 | 37.34 | 62.01 | 6.380 | 1.993 | 3.409 | 9.625 | 132.64 | 7.553 | 734.79 | 2.0564 | 0.0773 | 0.0000 | 0.8536 | 0.0691 |
| 2016 | 36.62 | 57.40 | 6.352 | 1.533 | 3.487 | 16.593 | 70.62 | 6.389 | 27.37 | 6.1389 | 0.1341 | 0.0000 | 0.8659 | 0.0000 |
| 2012 | 36.63 | 57.28 | 5.894 | 2.074 | 2.864 | 17.305 | 190.04 | 17.497 | 5589.23 | 2.2054 | 0.0000 | 0.0000 | 0.9503 | 0.0497 |
| 2008 | 35.13 | 61.54 | 6.490 | 1.889 | 4.790 | 34.722 | 52.33 | 10.115 | 21.48 | 9.7409 | 0.0000 | 0.0857 | 0.9143 | 0.0000 |
| 2004 | 37.21 | 59.71 | 6.846 | 1.951 | 4.529 | 10.919 | 58.25 | 1.541 | 14.39 | 0.9492 | 0.1959 | 0.0000 | 0.8041 | 0.0000 |
| 2000 | 35.08 | 57.67 | 6.562 | 1.795 | 3.912 | 34.448 | 68.55 | 4.673 | 26.02 | 3.6306 | 0.1554 | 0.0000 | 0.8446 | 0.0000 |
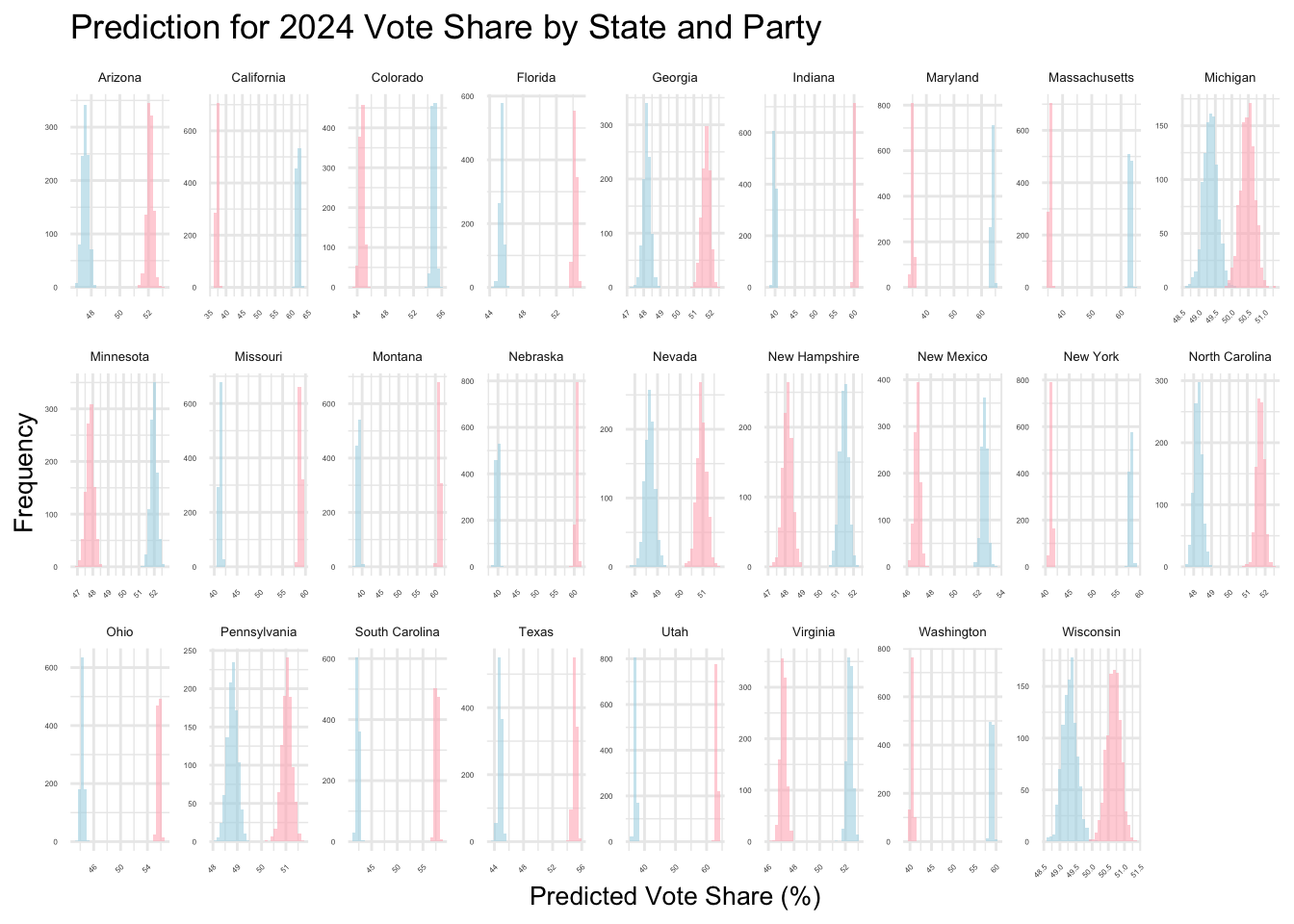
Similar to what I did for the national two-party popular vote share, I rescaled the predicted vote share to 100%. The columns in grey show the original values that do not add up to 100%.
| State | Rescaled Predicted Democratic Vote Share (%) | Rescaled Predicted Republican Vote Share (%) | Winner | Lower Bound (D) | Mean (D) | Upper Bound (D) | Lower Bound (R) | Mean (R) | Upper Bound (R) |
|---|---|---|---|---|---|---|---|---|---|
| Arizona | 47.73 | 52.27 | Republican | 47.20 | 47.58 | 47.94 | 51.75 | 52.11 | 52.48 |
| California | 62.42 | 37.58 | Democrat | 61.46 | 61.97 | 62.52 | 36.85 | 37.32 | 37.80 |
| Colorado | 55.13 | 44.87 | Democrat | 54.46 | 54.86 | 55.27 | 44.17 | 44.65 | 45.14 |
| Florida | 45.57 | 54.43 | Republican | 45.00 | 45.39 | 45.78 | 53.89 | 54.22 | 54.57 |
| Georgia | 48.23 | 51.77 | Republican | 47.83 | 48.19 | 48.53 | 51.31 | 51.72 | 52.09 |
| Indiana | 39.78 | 60.22 | Republican | 39.40 | 39.86 | 40.34 | 59.88 | 60.33 | 60.76 |
| Maryland | 64.66 | 35.34 | Democrat | 63.34 | 63.99 | 64.64 | 34.27 | 34.97 | 35.56 |
| Massachusetts | 63.93 | 36.07 | Democrat | 62.70 | 63.29 | 63.91 | 35.11 | 35.71 | 36.25 |
| Michigan | 49.44 | 50.56 | Republican | 49.01 | 49.35 | 49.70 | 50.12 | 50.48 | 50.82 |
| Minnesota | 52.08 | 47.92 | Democrat | 51.60 | 51.96 | 52.32 | 47.38 | 47.81 | 48.22 |
| Missouri | 41.25 | 58.75 | Republican | 40.89 | 41.34 | 41.79 | 58.43 | 58.86 | 59.29 |
| Montana | 39.01 | 60.99 | Republican | 38.54 | 39.04 | 39.57 | 60.59 | 61.03 | 61.49 |
| Nebraska | 39.67 | 60.33 | Republican | 39.32 | 39.83 | 40.32 | 60.07 | 60.57 | 61.02 |
| Nevada | 48.85 | 51.15 | Republican | 48.32 | 48.66 | 49.01 | 50.60 | 50.95 | 51.29 |
| New Hampshire | 51.66 | 48.34 | Democrat | 51.01 | 51.44 | 51.86 | 47.69 | 48.14 | 48.56 |
| New Mexico | 52.84 | 47.16 | Democrat | 52.09 | 52.51 | 52.93 | 46.44 | 46.87 | 47.27 |
| New York | 58.44 | 41.56 | Democrat | 57.56 | 58.00 | 58.44 | 40.84 | 41.24 | 41.65 |
| North Carolina | 48.26 | 51.74 | Republican | 47.88 | 48.25 | 48.64 | 51.36 | 51.73 | 52.09 |
| Ohio | 44.29 | 55.71 | Republican | 43.93 | 44.32 | 44.70 | 55.37 | 55.74 | 56.08 |
| Pennsylvania | 48.88 | 51.12 | Republican | 48.46 | 48.80 | 49.15 | 50.70 | 51.04 | 51.39 |
| South Carolina | 42.35 | 57.65 | Republican | 41.92 | 42.35 | 42.78 | 57.22 | 57.65 | 58.04 |
| Texas | 44.85 | 55.15 | Republican | 44.39 | 44.75 | 45.14 | 54.64 | 55.03 | 55.40 |
| Utah | 36.90 | 63.10 | Republican | 36.40 | 36.96 | 37.52 | 62.75 | 63.21 | 63.66 |
| Virginia | 52.59 | 47.41 | Democrat | 51.95 | 52.33 | 52.69 | 46.77 | 47.17 | 47.61 |
| Washington | 59.31 | 40.69 | Democrat | 58.51 | 59.00 | 59.48 | 39.98 | 40.48 | 40.97 |
| Wisconsin | 49.32 | 50.68 | Republican | 48.95 | 49.31 | 49.67 | 50.30 | 50.67 | 51.00 |
For states with insufficient data, and therefore not included in this prediction, I assume their electoral votes will go to the party projected by expert predictions from Sabato Crystall Ball, as shown in the map below. there are no discrepancies between my predictions and those from Sabato’s Crystal Ball, and I predict that all swing states will vote Republican.
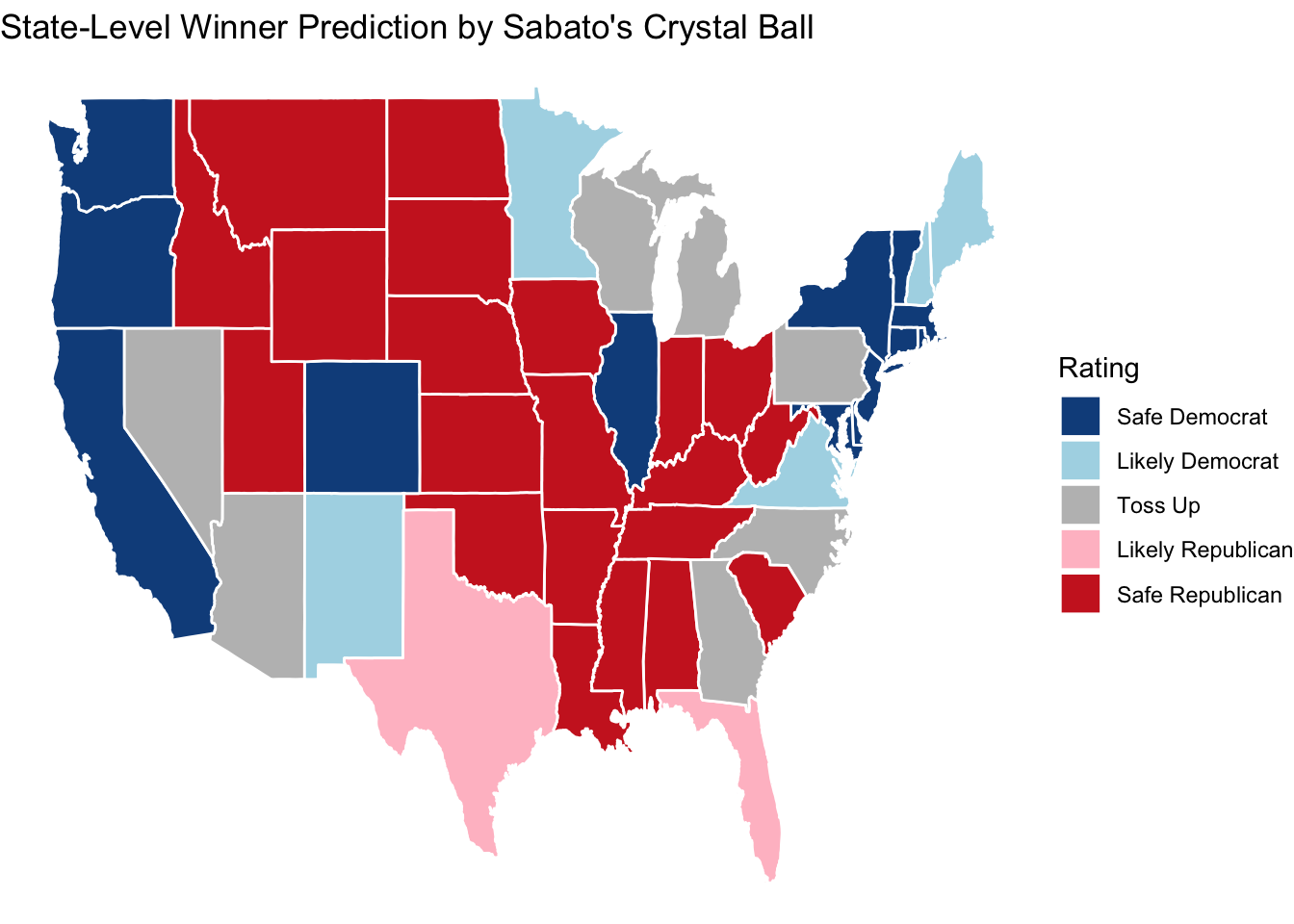
Therefore, my final prediction for the electoral college vote distribution by party is shown in the map below:
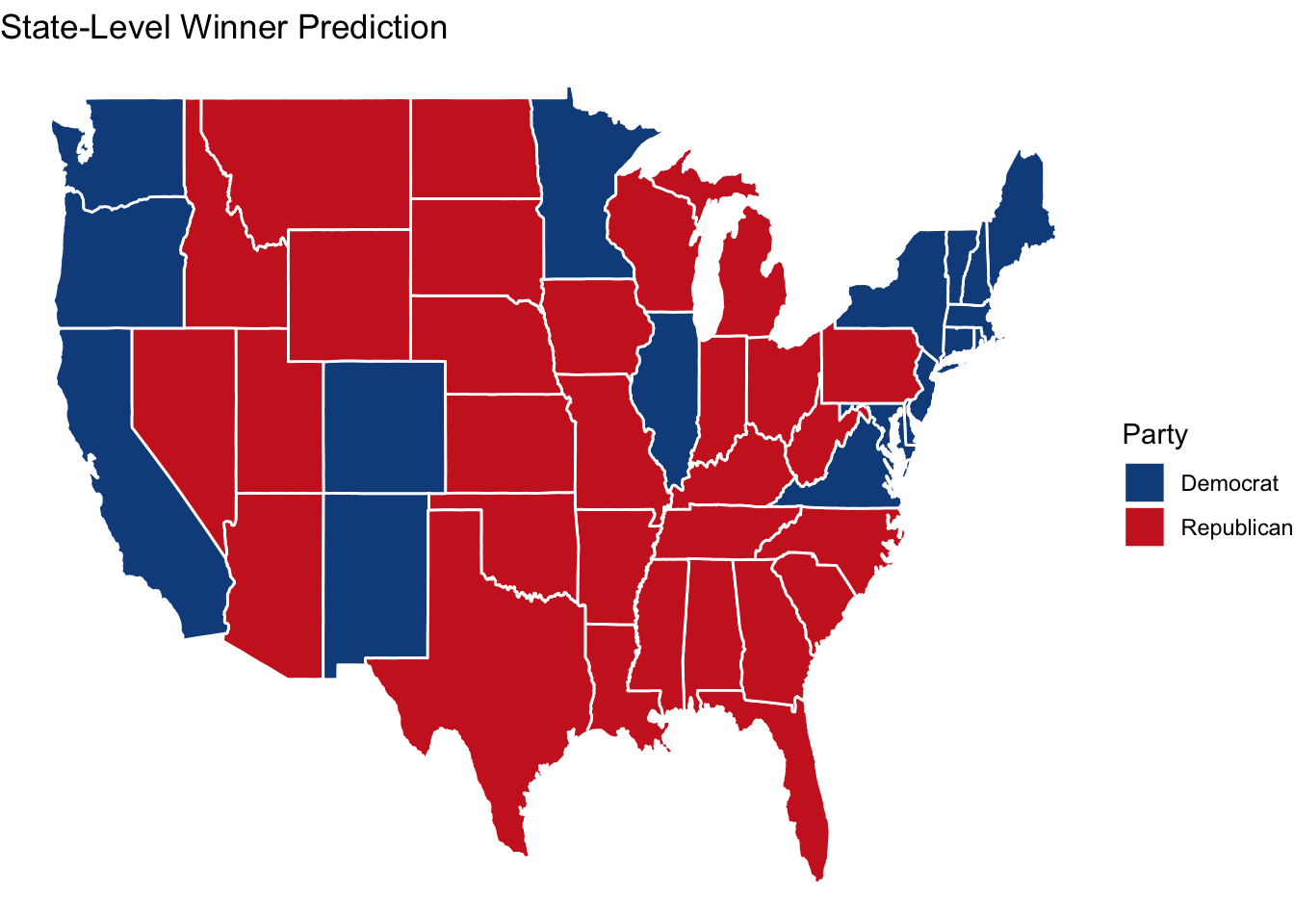
| Party | Total Electors |
|---|---|
| Democrat | 226 |
| Republican | 312 |
I predict that the Democratic Party will win the national two-party popular vote with a share of 56.76% compared to 43.24% for the Republican Party. However, despite this popular vote advantage, I anticipate the Democratic Party will lose the electoral college vote, receiving 226 votes compared to the Republican Party’s 312 votes. This would result in the Republican Party winning the Presidency and Vice Presidency.